자료의 요약

 단어가 데이터다. 클릭이 데이터다. 링크가 데이터다.

 오타가 데이터다. 꿈속에 나온 바나나가 데이터다.

 어조가 데이터다. 쌕쌕거리는 숨소리가 데이터다.
 심장박동이 데이터다. 비장의 크기가 데이터다.

 검색어는 가장 계시적인 데이터다.

 사진 역시 데이터로서의 모습을 드러냈다.

 - 모두 거짓말을 한다 -

 

---

 

 ▶ 커플들의 싸움을 일으키는 76%의 원인이 사소한 습관 때문이라고 합니다.

 ▶ 만약 당신이 "내 친구의 남자친구는 그렇지 않더라"는 발언으로 비교 평가하려 한다면 그 말을 잠자코 듣고 있던 당신 남자친구의 87%는 자괴감에 밤잠을 설칠 것이라고 합니다.

 ▶ 물론 그들 중 30%는 화를 내기도 합니다.

 ▶ 한번 헤어졌던 연인과 관계회복을 꿈꿨던 사람은 무려 82%에 달합니다.

 ▶ 헤어졌다가 다시 만난 커플의 해피 엔딩 가능성은 3%정도라고 합니다.

 

---

 

중앙값보다 평균이 덜 중요한 이유는 무엇일까요?

 

양 끝단의 값은 평균에 크게 영향을 미치기 때문에 통계에서는 평균을 잘 쓰지 않아요.

중앙값은 극단적인값의 영향을 받지 않는다는 장점이 있습니다.

즉, 성적이 엄청 높은 사람과 엄청 낮은사람을 신경쓰지 않기 때문이지요.

 

---

 

data<-read.table("table1_1.txt", header=T)

# txt파일을 읽어와서 data 변수에 저장합니다.

 

table(cut(data$age, br=seq(18,28,2), right=F))

#data에서 age열을 얻어와서 18~28까지 2씩 break해서 자릅니다.

#right가 False는 18~20이면 20과 같이 맨 뒤 값은 제외합니다.

 

table(cut(data$age, br=seq(18,28,2),right=F))

table(cut(data$age, br=c(4),right=F))

 

barplot(table(data$year))

#barplot은 테이블을 막대그래프로 나타냅니다.

#학년처럼떨어진것!! 질적변수를 표현하기 좋지요.

 

hist(data$age, br=seq(18,28,2), right=F)

#hist는 양적변수(범위)를 표현하기 좋습니다.

 

---

 

같은 교수님이 가르치는 A반과 B반이 있습니다.

두 반의 성적을 비교해볼까요?

 

1) table1_3.txt 읽기

 ▶ data<-read.table("table1_1.txt", header=T)

 

2) cut함수를 이용한 도수분포표

 ▶ table(cut(data1$A, br=seq(0, 30, 10)))
 ▶ table(cut(data1$B, br=seq(0, 30, 10)))

 

3) A와 B의 히스토그램

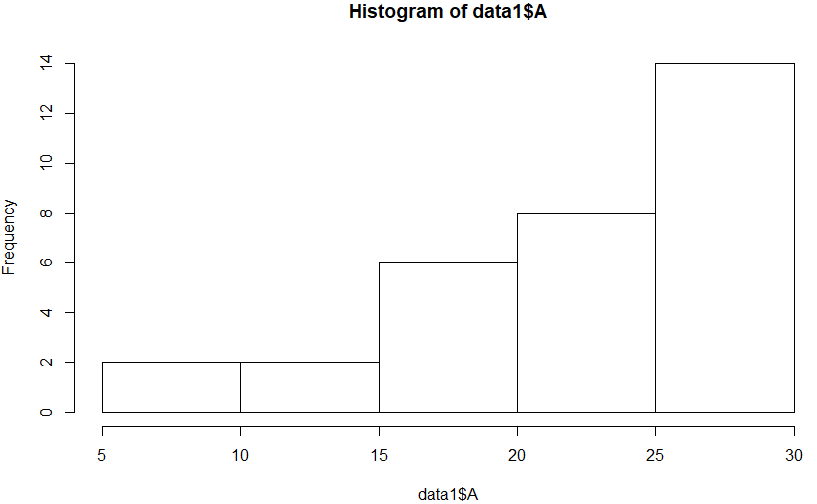
 ▶ hist(data1$A)

[그림1] hist(data1$A)

 ▶ hist(data1$B)

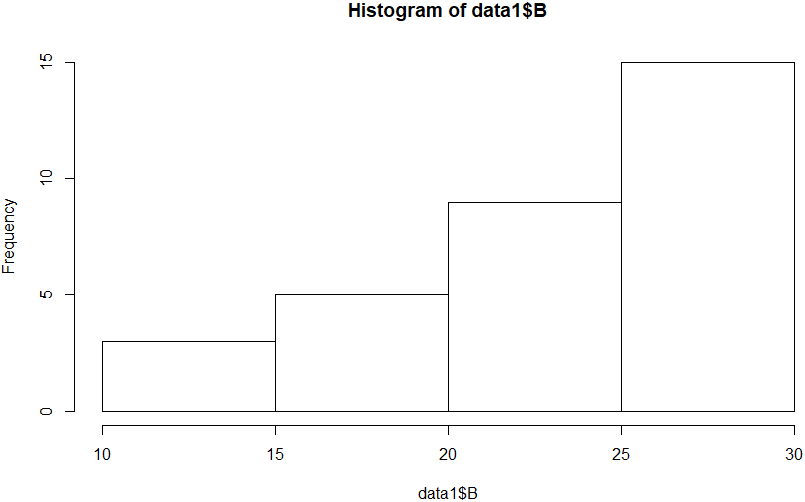
[그림2] hist(data1$B)

 

4) A와 B의 줄기잎 그림

 ▶ stem(data1$A)

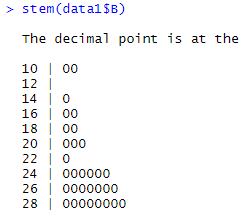
[그림3] stem(data1$A)

 ▶ stem(data1$B)

[그림4] stem(data1$B)

 

5) A와 B의 상자그림

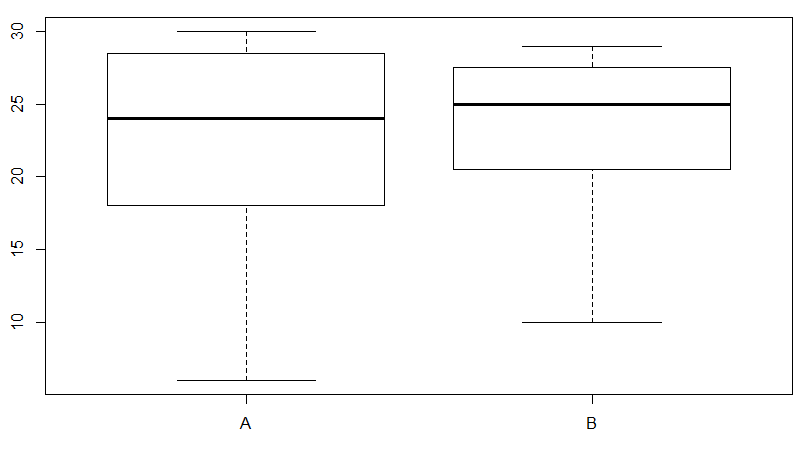
 ▶ boxplot(data$A, data$B, names = c("A","B"))

[그림5] boxplot(data1$A, data1$B, names=c("A","B"))

 

6) A와 B의 비교분석

A반에 비해 B반의 중간값이 높고, A반은 특정 한 두 사람이 잘하지만 나머지는 잘 못하는 것으로 보입니다.

즉, 개인적으로 각자 열심히 하는 것으로 보이며, B반의 경우 분포가 잘하는 사람과 못하는 사람의 편차가 A반보다 낮은 것으로 보이는 부분에서 함께하는 응집력이 높은 것으로 보입니다.